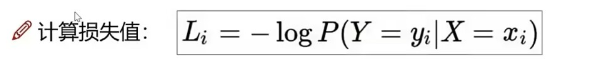深度学习 其二 神经网络和卷积神经网络

深度学习 其二 神经网络和卷积神经网络
fufhaha深度学习 其二 神经网络和卷积神经网络
传统算法(机器学习)流程:数据获取->特征工程(人为筛选特征)->建立模型->评估与应用
传统:{我觉得,我认为}
深度学习:不需要自己去判断哪个特征合适,全部交给计算机—》end ~ end 端到端
一.计算机视觉:
计算机视觉:—》一张图片被表示为三维数组的形式,每个像素值从 0-255
如:300 *100 *3–》》每个像素点值越小表示表示这个点越暗,反之越亮
那怎么把数据转化为特征?图像->向量(每个算法的核心是特征是怎么去做的,就是怎么将数据转化为特征的)
Ecoder–》特征怎么做的好
Dcoder–》怎么用特征去得到一个输出结果
很多数据集中的标签都是仿真去采集的
传统神经网络:
假如有一个 32*32 3 的一个矩阵表示的图像数学数据 32 * 323=3072—>神经网络会把这 3072 个像素点展开成一列的向量形式,也就是有 3072 个特征—–>接下来设置一列权重(3072)对 W 和 x 求矩阵—-》注意,神经网络最后输出的是属于各个类别的概率,每一列 W 都代表一种类别(如猫,狗),可以重新再设一组 W 代表其他的类别,如果有 10 个类别,就要有 10 组权重参数矩阵—->最终输出 10 个类别分别的概率值+偏执(偏执的数与输出挂钩,所以偏执这里有 10 个)

数值-x 低效—>矩阵计算

首先 W 是权重参数,这是随机初始化得到的,但是这时会遇到一个问题:初始化的有时好有时不好,这怎么办?
–>预训练模型:我们可以用别人训练好的参数做初始化
b–>偏执,主要是 W+xi 后对数据再次的微调,但影响不大,核心还是权重部分
最后得到预测结果—>最后图中属于猫的预测值不高,这时,我们要调节 W—》损失函数
想要训练好:
–>batch 要大(看其一,就是单次循环的操作数据图的个数) 128—>求这一批的平均值,详细看【其一】
损失函数(一些基础细节见【其一】)
损失函数不是固定的,他可以是由我们来定义的(我们自己需要在模型中关注什么),许多创新,突破效果的东西都可以从损失函数入手
->就是把预测的与实际的数据相对比,加上很多约束条件,然后看与约束条件的匹配程度

正则化:

虽然结果值相同,但是模型还是不一样的,w1 偏科,最好选 w2—>那怎么让计算机知道我们要选 w2 呢?—->正则化惩罚
比如这里面的 w1 突然忽大忽小的,而 w2 相对比较平稳,这时加上一个 L2 正则化—>最各项平方求和
即 w1->1 ,w2->1/4.这时最值大的惩罚大,我们就选择正则化惩罚小的第二个模型
当权重参数出现忽大忽小->多因素,样本有特例(尖端)—>最好人工的进行删一点,算法上修改的话不怎么好,同时 batch_size 要大一些,取平均值,稳定一些
—>正则化损失项一般会和损失函数加在一起
损失函数=数据损失+正则化惩罚项

1.分类损失函数:—–看论文—>网络结构,损失函数

公式看不懂的话可以画出来
softmax 分类器—>把得分值转换为一个概率值:–>可控,稳定上升,有限制
这个分类器就是一个函数公式吗?0-1—>如果要 0-4 可以选择平方或者*4(先用 0-1 表示,然后为了结果做一个映射)
siymod 函数

exp—>指数次幂映射—>让数据的数值取值范围更大些(拉开数据的差异后再进行 softmax 分类)
计算损失值:用对数来,错的越多,离 1(x)越远,最后一项看的是损失函数的损失值
前向传播:(基础看【其一】)
直到达到最低点,梯度为 0,W 调整到最优值
adam
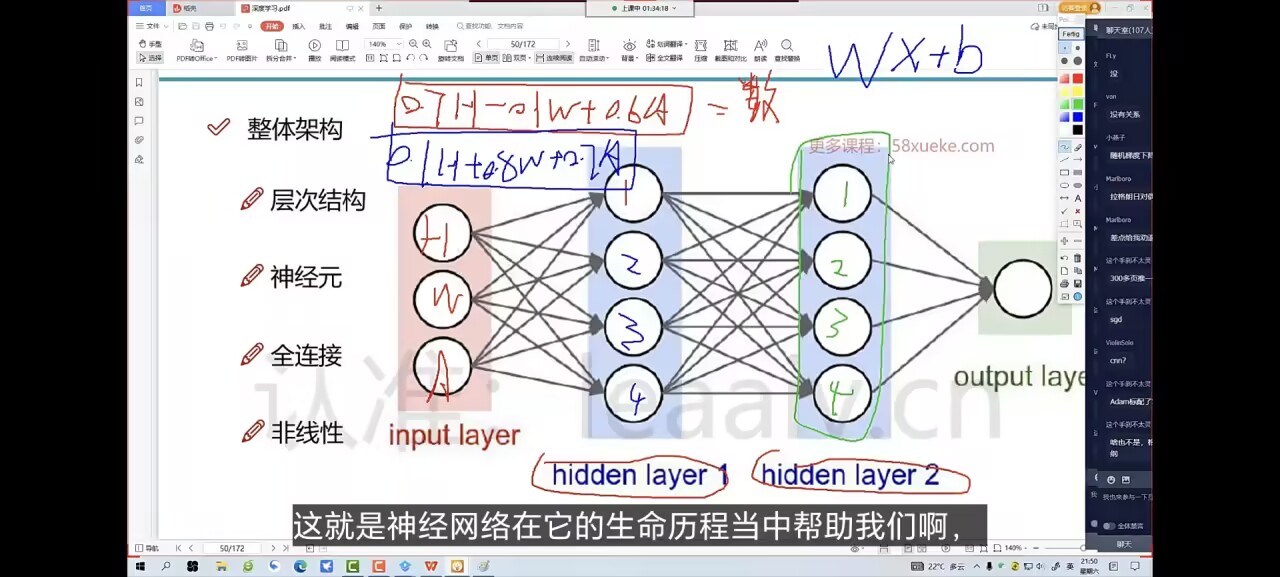
神经网络整体结构:
只管输入和输出,中间全部由计算机完整
激活函数:
激活函数加在每一个神经元的输出处,就是给神经元输出加上一个非线性的变换函数,让神经元能输出更复杂的东西(为什么这样就能输出更复杂的东西,难道不怕输出后的结果更偏离了正确吗?),神经元就是隐藏层中的每一个点,如上图中的圆点,红色是输入神经元,蓝色是隐藏层神经元,绿色是输出层神经元
常见的激活函数:
| 名称 | 公式/表达式 | 主要特点与应用 |
|---|---|---|
| Sigmoid | ( f(x) = \frac{1}{1+e^{-x}} ) | 输出范围(0,1),早期常用,易梯度消失 |
| Tanh | ( f(x) = \tanh(x) ) | 输出范围(-1,1),比 Sigmoid 好一些 |
| ReLU | ( f(x) = \max(0, x) ) | 目前最常用,收敛快,简单高效 |
| LeakyReLU | ( f(x) = \max(0.01x, x) ) | 解决 ReLU”死神经元”问题 |
| Softmax | ( f(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} ) | 多分类输出层常用 |
数据预处理:
1.标准化:
去均值,让其对原点中心对称
但是发现过于散,让各个维度取值范围尽量相同—>标准化:各个维度更均衡
过拟合:
只学其形,未获其神:模型在已有数据训练的很好,但是在新的数据上效果不理想,只记住了死数据,没有找到规律
DROP-OUT:防过拟合–用的特征越多就越容易过拟合,这个可以删减部分特征,随机”丢弃”部分神经元的方法。
具体是:按照一定比例如 0.5 在一次训练中让一定的神经元在前向传播和反向传播中失效,不参与

原理 1:防止神经元”抱团作弊”
如果没有 Dropout,某些神经元可能会”抱团”,只要它们一起出现就能记住训练集的某些特征,导致模型只会”背答案”。
Dropout 让神经元每次都要”单打独斗”,不能依赖其他特定神经元,这样模型只能学到更”通用”的特征。
原理 2:等于训练了很多不同的子网络
每次 Dropout 都会产生一个不同的”子网络”,相当于在训练过程中集成了很多不同的网络。
这样模型不会过度依赖某些特定的参数,提升了泛化能力。
原理 3:减少模型复杂度
- Dropout 相当于让网络在训练时变”稀疏”,有效减少了模型的复杂度,降低了过拟合风险。
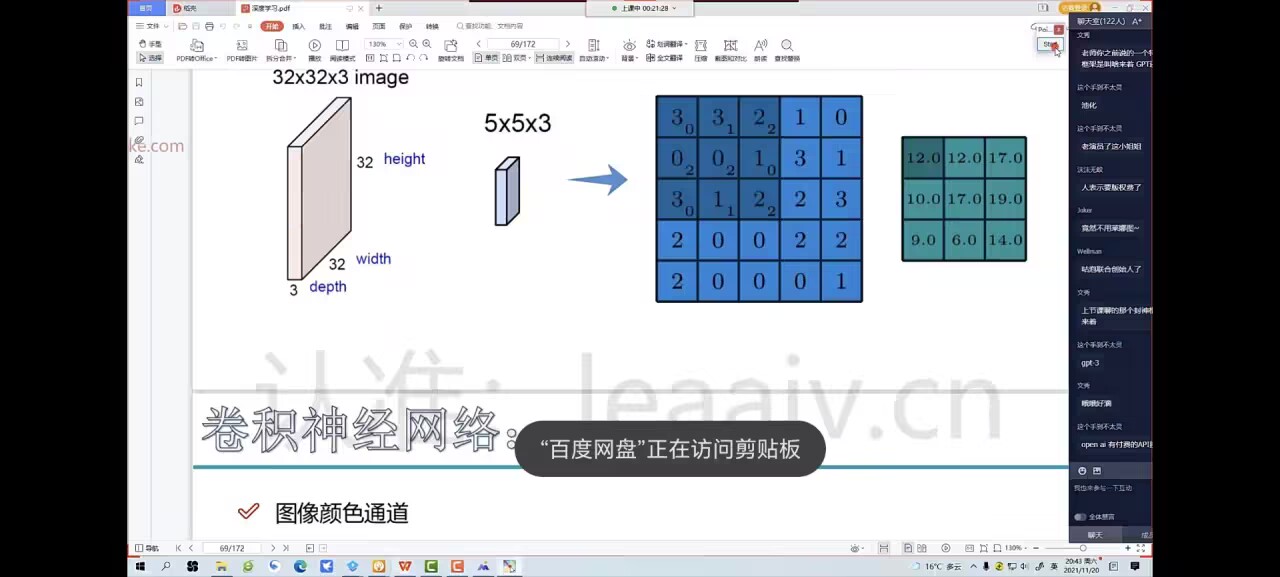
卷积神经网络(CNN):
怎么卷?
在一个像素点矩阵中指定一个区域,提取这个区域的一个特征值,然后特征值再构成一个矩阵,。
- 卷积核是用来提取特征的”权重矩阵”,是网络要学习的参数。
- 卷积核本身不会变,特征图会随着输入图片不同而不同。
- 每次滑动时,把卷积核和该区域的像素做加权求和,得到一个新的数,这个数就是”特征值”。
一个区域可以提取 n 个特征
卷积中第三个维度一定要和输入的第三个维度一样,其余 2 个维度可以自定义 –[高, 宽, 通道]
内积:比如两个垂直的独立无关的向量,内积一定为 0 相关性越大,内积就越大
内积就是卷积核提取特征值的核心操作:如神经网络里面的,特征值=W*x+b,这个 w * x 就是内积的操作
一个个像是滑动窗口一样进行计算特征值—+pad1,为了公平,所以外围+0
1. x 是什么?
在卷积操作中,x 就是输入的像素值。
对于一张图片来说,x 就是某个小区域(比如 3x3 窗口)里的所有像素点的值。
如果是灰度图,就是单通道的像素值;如果是彩色图,就是每个通道的像素值。
2. w 是什么?
w 就是卷积核的权重参数,也是神经网络训练时要学习的参数。
在网络刚初始化时,w 是随机生成的(通常是高斯分布或均匀分布的随机数)。
随着训练的进行,w 会不断被优化,最终学到能提取有用特征的权重。
w 组成的矩阵就是卷积核
1 | [[w11, w12, w13], |
卷积核越小越好,越多越好,可以设置多个卷积核提取多个特征的特征图
卷积当层是在上一层的基础上整合特征去做的

卷积结果计算公式:

卷积参数共享:
虽然卷积参数对每个不都适用,但如果每个卷积核操作都设置一个参数,学起来太慢了

池化:c 不变—压缩,w,h 压缩为 n 倍
卷积太多了,要压缩,就是池化—pool

最大池化:

把重要特征的数值取越来越大,即池化压缩的时候选最大的,一般是最大池化,其他也可以,不多
(卷积(conv)->激活->卷积->激活->池化)*2->输出
由权重参数计算才能称为一层卷积,例如,下图有 7 层:

特征图变化:

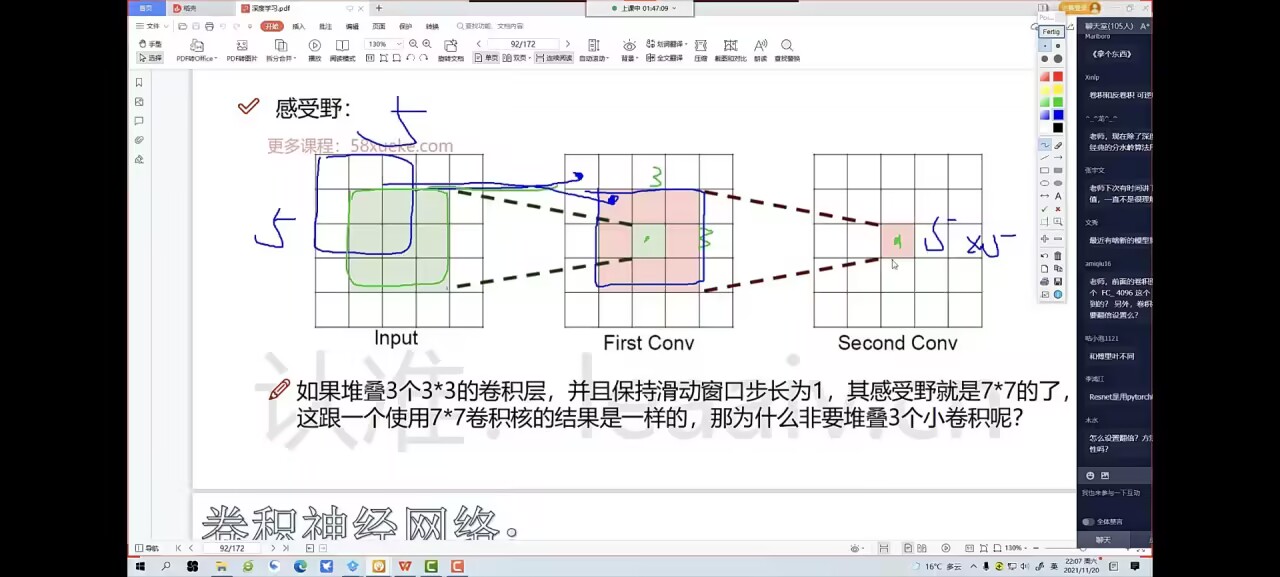
感受野:
感受野会随着卷积的层层进行不断增大,就是前 n 个权重参数的个数